How k-means clustering is used to identify customer personas

Using machine learning to identify customer personas in your data can help improve your understanding of your customer base, and with the right infrastructure, deliver personalized experiences at a greater scale.

In a nutshell, the process entails using an algorithm to segment your customer data into distinct groups, or personas. Faraday uses a time-tested method called k-means clustering.

What is k-means clustering?

K-means clustering is an unsupervised clustering algorithm that was first introduced in 1957. An unsupervised algorithm does not require the data to be labeled in order to train the model. This is an important feature of the k-means algorithm because it allows for the discovery of subgroups within the data without any previous assumptions about possible groupings — in this case, personas.

How does k-means clustering work?

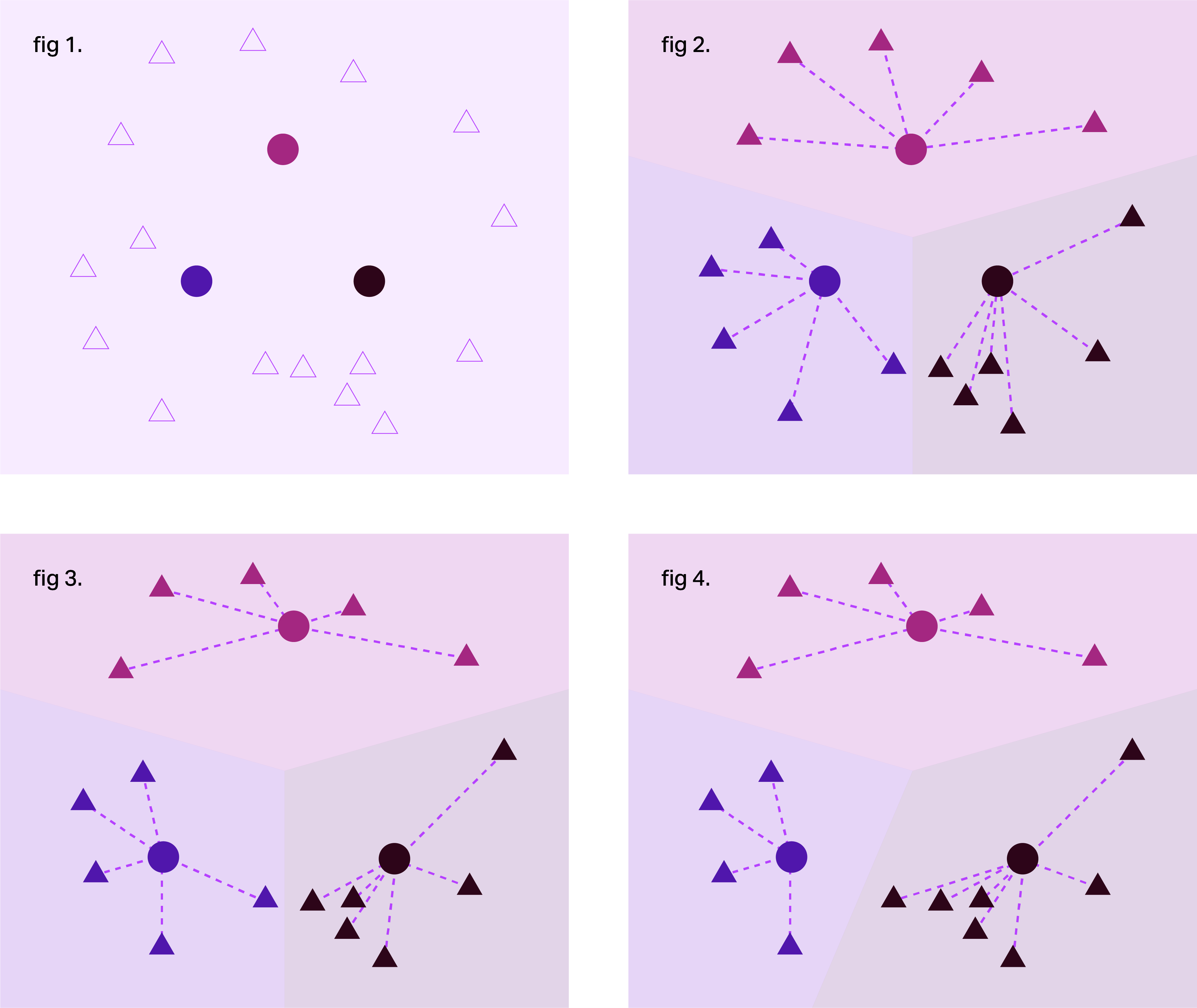
When presented with a data set, the k-means algorithm first introduces random center points around which each data point will eventually be clustered (circles, Fig. 1). Then each data point is assigned to the group of the center to which they are closest. This happens by calculating the distance from a data point to each cluster center using an equation known as the Euclidean distance measure. For two dimensions, the Euclidean distance is represented by the diagonal line connecting the point to each of the cluster centers. The point is then assigned to the cluster center with the shortest diagonal line (Fig. 2).

Once each point has been assigned to the randomly chosen cluster centers, the centers then "update," moving to the center of the group by recalculating the mean (average) distances to all the points in the group (Fig. 3).

After the cluster centers have updated to their new positions, each point is reassigned to a new group using the Euclidean distance measure again. Most of the points will remain in their original groups, but some points will be assigned to a new group (Fig. 4). So, then the centers must be updated again to be at the center of the new group. This pattern repeats until the centers no longer move.

Using k-means clustering for customer personas

All of the above is how k-means clustering worked back in 1957. Since then there have been upgrades allowing us to use something called categorical features. At Faraday, we create persona groups using a mix of these features.

As far as algorithms go, k-means is rather straightforward, but has one major downfall: you have to tell it how many groups to look for, and it will always succeed in finding that many groups. That means if you tell the algorithm to look for 500 groups, it will find them — even if there is no reason for there to be 500 distinct groups within the data.

If you're a marketer, you probably don't want to create 500 unique ads for every campaign. But should you make four? Or six? Or ten?

How to find the optimal number of personas using k-means clustering

We target the optimal number of groups hidden within the data, rather than guessing and hoping we are right. We’ll share a few methods we use to find the optimal number of personas for our users.

The elbow method: finding diminishing returns

The most common metric for measuring the success of k-means clustering is called the ratio of sum of squares (rss). At Faraday, we determine the optimal number of personas by comparing the rss for k-means models with two to fourteen personas. We employ the elbow method, which shows the cutoff after which we see diminishing returns for increasing the number of personas. For most clients, the optimal number of distinct personas is usually between four and seven.

Going beyond the elbow method

The elbow method is simple, but it has a downside: sometimes, there just isn't a clear single point that is optimal. Maybe three personas could be optimal, maybe six, and we have to intervene based on our client’s business needs to choose one or the other as the optimal number of personas.

Additionally, while reducing variability within each group is an extremely useful way to measure k-means clustering success, it doesn't tell the whole story. We believe that an important aspect of clustered groups is stability, which isn't considered with the elbow method selection process. Our clients expect that their persona groups won't shift every time they convert a lead. This is why we are currently researching a new method for determining the optimal number of personas, which focuses on the stability of the persona group.

The bootstrap method: focusing on stability

Our first step to assess the stability of k-means clustering involves resampling the client’s data using the bootstrap method. Like k-means clustering, bootstrapping has been around for a while – it was first introduced in 1979 by Bradley Efron. The basic idea behind bootstrapping is to take data from the pool we have, with the ability to pick the same data point multiple times. This is a method known as sampling with replacement.

The bootstrap method provides us with a powerful tool to measure how much our desired clustering outcome could change with different data. We can get a good sense of how much the personas will change with the addition of new customers. Our goal is to minimize how much influence single customers, or small groups of customers, have on the resulting personas. We want personas that remain relatively unchanged by single customers. In other words, we want more stability.

Pulling it all together

Once we have the results from bootstrapping, we use the ratio of sum of squares again to measure just how stable the personas are. What we’re looking for is a ratio close to 1, which would indicate that there is no variability within the personas.

The stability metric for determining the optimal number of personas shows promising results for the basic examples in this blog post. At Faraday, we’re actively working on applying this methodology to the more complex persona groupings our clients rely on. Stay tuned for more developments with respect to improving our personas methodology.