Geonormalization in Faraday
At Faraday, we automatically detect and correct for geographic bias in our training data through a process we call “geonormalization”.


At Faraday, we automatically detect and correct for geographic bias in our training data through a process we call “geonormalization”.
Why geonormalize?
It's easiest to explain through some examples, so let's walk through two.
Example 1: to re-balance an unbalanced training population
Say you have a business with two customer bases: California and Nebraska. The business started in California, so its customer base in California is 10x what it is in Nebraska. Without geonormalization, because the business has more customers in California and those customers look totally different from those in Nebraska (e.g. higher household income in California), everyone in California is scored higher than those in Nebraska.
Example 2: to allow for a prediction to generalize over geographical areas not covered in the training data
If your business started in New York, so all of your data–demographics, financials, and so on–is New York-based, and now you're trying to find brand new business in California, the predictive model won't have been able to learn about what makes California unique in terms of that data, so the model will struggle to learn and its predictions will be unreliable.
Neither scenario is particularly helpful for growth!
Geonormalization adjusts both of these types of geographic bias with geography-based scaling instead of a raw value: Jane Doe is in the top 10% of scores in her state instead of the top 10% of scores for everyone.
Without geonormalization, you might define someone as "wealthy" if their net worth is $500k. Having a definition this static can present problems when comparing people from different demographic and financial backgrounds. With geonormalization, and keeping the above examples in mind, the definition of wealthy becomes more dynamic: "they have a net worth over twice as much as the average in their county."
Just because someone lives in a location that’s different from your customer data doesn’t necessarily mean that they should score lower than everyone that resembles your customer data.
How does Faraday geonormalize?
Hence the need for a correction factor, to ensure that we are able to find the most likely customers in all of the regions our client wants to expand into. Our approach requires a detection algorithm and a correction algorithm.
Detection
We use a simple, but effective, algorithm. We compare the market penetration (customers / total possible customers) among each distinct geographic area at the desired level of analysis. If the largest market penetration is greater than 100x the smallest market penetration then we perform our correction algorithm during training.
For detections we start at the largest geographic area of interest, the state level, and work our way down to the smallest geographic area of interest, the postcode level. If at any point during the detection, the 100x threshold is met we perform the correction for that geographic level. Therefore, we are always applying the correction at the largest level possible.
Correction
We use a two-pronged approach to correction: instance weighting for the training examples, and bias correction for the training features.
Instance weighting
We assign a weight to the positive examples calculated from the penetration rate of those positive examples in their respective geographic area. This in essence levels the playing field and gives a boost to the positive examples from areas where there are relatively fewer examples (unsaturated markets) and gives a penalty to the positive examples from saturated markets.
From a modeling perspective, we are tricking the model to believe that the good examples are just as likely to exist in any of the geographic segments. This leads to less bias amongst the features used to distinguish good examples from bad examples.
Feature correction
Our other method we employ in tandem with the instance weighting, is to transform features so that we level the playing field across the geographic segments. Instead of providing the model with raw features, we transform them so each person is represented by the percentile they occupy within their segment. Again, this one is probably easiest to explain via an example.
Instead of providing raw household income values of $84k for CA resident A and $66k for NV resident B, we provide the model with how they rank amongst their peers within their respective states. I’ve chosen the median income for each state, so the model would receive 50 for resident A and 50 for resident B.
By correcting the features, we provide the model with fewer discriminatory features with which to determine that everyone from the more saturated geographic segment is a better fit than everyone from the less saturated segments.
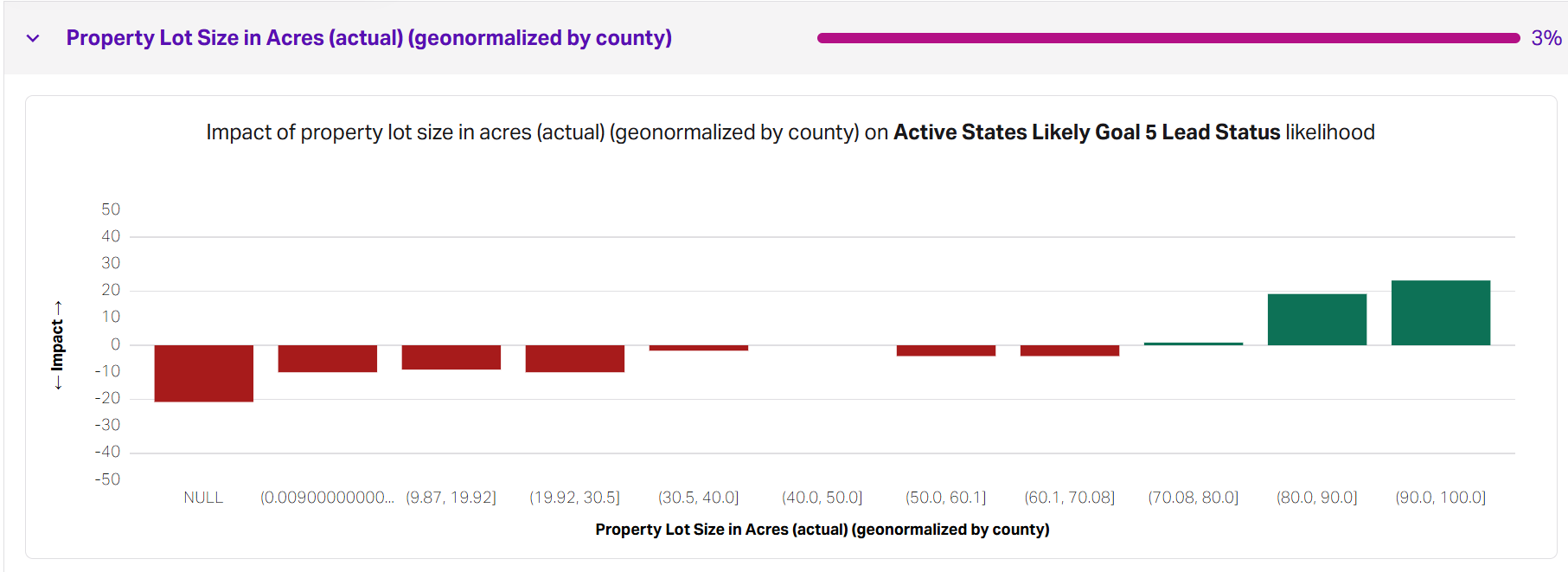
Interpreting geonormalized datapoints in Faraday's dashboard
When a feature is geonormalized, it means the model is looking at how someone compares to others in their local area—not just at the raw value.
In the Faraday dashboard, when you see a feature labeled as “geonormalized,” the x-axis will show percentile ranges, not raw values. This is because the model is evaluating where an individual falls within their local geographic distribution. So, a range like 80.0, 90.0 on the x-axis represents people whose property lot sizes are in the top 10–20% within their own county, not people with a specific number of acres.
That’s why the chart might show higher likelihoods of attainment in the top percentile buckets—because being in the top 10% locally often signals above-average wealth or property characteristics for that area, even if they have less than those in a different region. This approach lets the model surface meaningful patterns without over-weighting regions with more or denser data, and ensures you're interpreting datapoints relative to local norms, not national ones.
Conclusion
Geographic bias correction, or “geonormalization”, means that when using Faraday to expand your business into new markets, you can do so confidently knowing that our models will not just default to recommending people from markets in which you already have a significant presence. Grow your business confidently with predictions from Faraday.

Brendan Whitney
Brendan Whitney is a Senior Data Scientist at Faraday, where he identifies and manages feature development projects for Faraday’s modeling pipeline infrastructure. He also shares knowledge on novel modeling techniques through blog posts and documentation and brings deep experience designing, maintaining, and improving Faraday’s statistical modeling systems. Brendan holds an MS in Complex Systems and Data Science and a BS in Data Science and Mathematics from the University of Vermont.

Ready for easy AI?
Skip the ML struggle and focus on your downstream application. We have built-in demographic data so you can get started with just your PII.